Attention, ceci est un avertissement ! Que tous ceux à qui les mathématiques, statistiques et autres opérations hérissent le poil cessent de lire ces lignes : vous allez entrer dans la partie sombre de Magic, celle de l'inconnu et de l'imprévu. Je vais vous montrer le lien entre les statistiques et Magic. Car rappelons-nous : Richard Garfield était, à la base, prof de math...
Quoiquoiquoi ?
Quand on builde un deck, on se demande combien d'exemplaire de chaque carte faut-il y mettre. On va forcément me dire que pour les cartes indispensables, il faut les mettre 4 fois. Mais est-ce vraiment vrai ? Naturellement, on se dit qu'il suffit de la mettre en 4 exemplaires pour être sur de l'obtenir dans la partie. On a alors 4 chances sur 60 de la piocher n'est-ce pas, donc une chance sur 15. FAUX, archi-faux ! La vraie formule n'est autre que :
Bon, ben ça y est, à tous ceux qui ont vomi en lisant la ligne précédente, je vous avais prévenu... Pour les autres expliquons un peu... La probabilité de tirer au moins une fois une carte, c'est égal à la probabilité de tout les événements possibles moins celle de ne jamais tirer la carte en question. Et la probabilité de ne jamais tirer la carte, si on l'a en 4 exemplaires, c'est à la première pioche de 56/60, puis de 55/59, puis 54/58, et ainsi de suite... Formulée avec des exponentielles, c'est ainsi que l'on obtient la formule bien précédente à vous donner de l'urticaire. Et ça change quoi ? Ben que la proportion des chances de tirer la carte n'est pas celle que l'on imaginait, et que bien sur, elle augmente au cours du temps. Parce que forcément, quand on a pioché la dernière carte, si tu ne l'as toujours pas trouvée, poses-toi des questions sur le type qui a demandé à jeter un coup d'œil à ton deck tout à l'heure...
A quoi ça a servi que je vous explique tout ça ? A vous donner une raison de changer le beau PC sur lequel vous venez de vomir en lisant ces lignes, à vous acheter des aspirines, et à comprendre la suite.
Et en gros, ça donne ?
Voici donc le graphique représentant tout cela (merci matlab): la courbe en haut représente la probabilité en fonction du tour auquel on pioche la carte d'avoir obtenu jusqu'à présent au moins un exemplaire de la carte voulue. En bas, si l'on a un seul exemplaire.
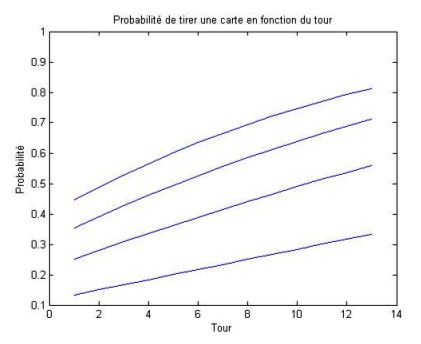
Tout ça en ayant prit en compte le fait qu'on a d'abord pioché 7 cartes au début. En gros, ça rapporte qu'on a environs 60 % de chances d'avoir tiré la carte au 6é tour si elle est en 4 exemplaires. 20 % si elle y est en 1 seul. Et pour savoir, si j'ai 2 tuteurs et 3 exemplaires de la carte nécessaire, j'ai environs 70% de chances de pouvoir l'avoir avant le 5é tour.
Tout ça, c'est « important » pourquoi ? parce qu'on se rend compte que pour un jeu optimal, on a pas besoin de mettre une carte en 4 exemplaires alors qu'on en a pas besoin avant le sixième tour. La mettre en 3 fois au lieu de 4, ça libère un slot. Et deux fois comme ça, ça fait 2 slots. Ca sert parfois pour les jeux combos ou contrôle. Parce qu'avoir trop de chances d'avoir une carte injouable avant longtemps dans la main, c'est pas toujours utile. Parce que si j'ai besoin de deux cartes différentes au 6é tour pour mon combo, sans tuteur ou quoi que ce soit, si elle y est en 4 exemplaires chacune, ça fait à peu prés une chance sur 3 de l'obtenir. Donc, les piocheurs, c'est sacrément utile aussi...
On parle de Combo ?
Pour calculer les probabilités de réunir un combo, il suffit de multiplier les probabilités entre elles (cela ne sera pas exactement juste, mais ce sera une bonne approximation). Par exemple, si je veux réunir mon combo Hommage de sang + Lien sanguin + vampire, disons que j'ai besoin d'avoir pioché les 3 cartes au sixième/septième tour (6é pioche donc). Voici un graphe de la probabilité de la réunir, en fonction du nombre de Lien sanguin dans mon deck, si j'ai 2 hommages de sang et 8 vampires :

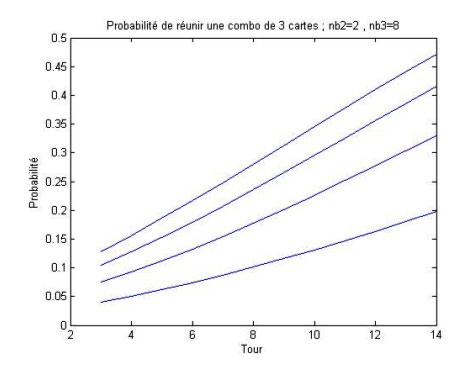
Moi qui met 3 Lien Sanguin dans mon deck, ça me fait 1 chance sur 5 de tout avoir (et de gagner la partie ^^) au septième tour. Il s'agit d'une approximation, car le fait de piocher une telle carte influe (légèrement, puisqu'on en a 60) sur les chances d'en piocher une autre.
Ensuite, quelques graphes pour des combos diverses :
Combos de 2 cartes : nb2 est le nombre d'exemplaires de la 2é carte du combo dans le deck
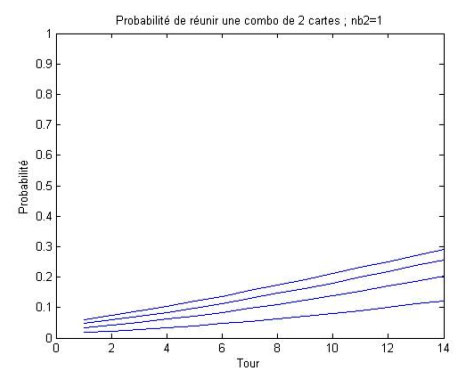
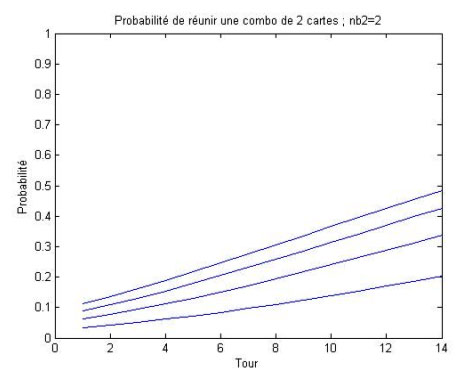
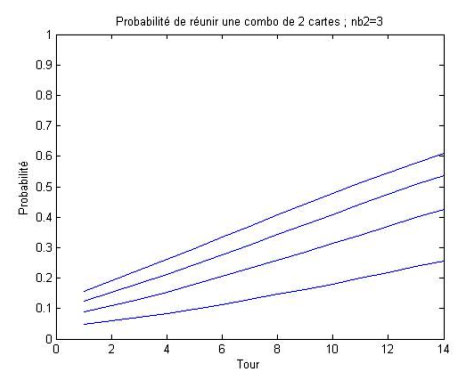
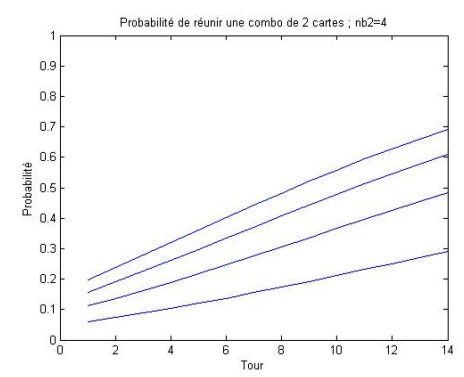
Combos de 3 cartes : nb3 est le nombre d'exemplaires de la 3é carte du combo dans le deck
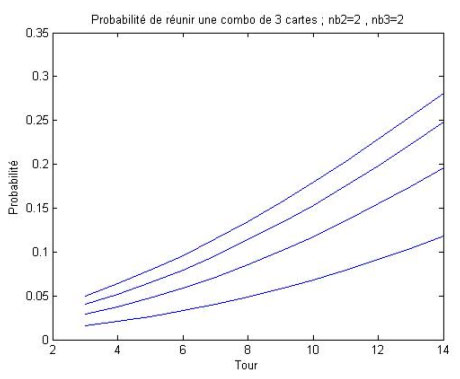
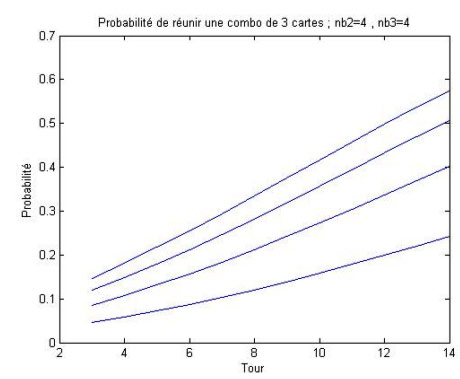
Et on pourrait en faire pleins d'autres comme ça, mais ça devient trop lourd (graphes à X dimensions...). Retenez juste qu'il suffit de multiplier les probabilités d'obtenir chaque carte séparément pour obtenir la probabilité totale de réunir toute les cartes.
Attention, il ne s'agit que des chances de piocher les cartes en question, pas de pouvoir les utiliser, car il faut piocher du terrain alors... De la proba en plus à calculer...
Donc, si je veux avoir la combo Boule de feu + Transfert + Black Lotus dans ma main de départ, avec 4 Channel et 4 Fireball, et un Black Lotus, ça fait... environs une chance sur 50... Y'a d'l'espoir !
OK, on s'est cassé les ****, acheté de l'aspirine, et tout ça pour comprendre ces lignes... Mais j'ai appris quwé ? Ben :
- Les chances de tirer une carte ne sont pas toujours celles que l'on croit
- Pour ceux qui en doutaient encore, la pioche c'est important, les tuteurs aussi
- Pas toujours besoin de mettre 4 exemplaires de chaque carte
- Un peu de math...
- Lire quelques graphes ennuyeux...
Hé bien voila, on a fini. Pas si hard que ça heing ? Quoi ? Vous saviez déjà qu'il faut mettre des tuteurs et des piocheurs dans son deck combo ? Ben au moins maintenant je vous aurais démontré pas a+b que c'est nécessaire, nah !

5 points
Le 06/06/2011
des fois la proba de piocher un des carte de la combo tombe au milieu de ton tour, mais comment tu a fait pour piocher au milieu de ton tour, c'est a dire entre ta phase de déclaration des attaquant et la phase de déclaration des bloqueur ?
Note : 9/10
85 points
Le 17/02/2010
Venitien, ya un truc que je comprends pas, j'execute ton calcul avec un exemplaire de carte et lors de la 1ere pioche et je trouve "un nombre négatif fois 10^27" O.o
alors soit je me suis loupé malgré 3 relectures soit excel est mauvais soit c'est moi qui suis mauvais et qui ne comprend pas.
Une idée?
254 points
Le 15/01/2010
Merci pour ton explication sur la factorielle Elvariand. J'aurais du effectivement le citer. Pour N, dans la formule, tu ne te trompes effectivement pas: c'est le nombre d'exemplires de la carte recherchée dans le deck.
Pour la meule, attention: effectivement, ça revient à avacer les tours, mais tu ne pioche pas la carte. Donc, tu dois plutot calculer la proba que la carte voulue soit dans les cartes meulées, faire une soustraction à la proba qu'elle soit encore dans le tas restant aprés (je crois). bref, c'est compliqué.
Pour la conversion en %, désolé de ne pas y avoir pensé. pas fait attention sur le coup.
Rappellez vous qu'il s'agit de graphes surtout à titre indicatif. Forcément, avec tout les aléas des match, meule, pioches, et cartes bizaroides que nous fourni wotc, dur dur d'avoir une pioche "normale" XD
85 points
Le 14/01/2010
Apres reflection, N doit plutôt être le nombre d'exemplaire de la carte.
Desolé désolé mais si Venitien voudrais bien confirmer mes dires, ce serait sympa ^^
85 points
Le 09/01/2010
Je pense que tu aurais dû expliquer un peu la ligne de proba pour les non-matheux... Voici pour ceux qui n'ont pas compris, ce que j'ai deduis de la formule :
60, c'est le nombre de cartes au départ dans votre deck donc si vous avez 130 cartes, il faudra faire le meme calcul en remplacant les 60 par des 130.
n correspond au nombre de cartes restant dans votre bibliothèque
t doit correspondre au nombre de tour donc tour 1 (t=1), tour 2(t=2)...
et pour les vraiment rebelles du calcul , le symbole " ! " correspond à la notion de factoriel. J'explique. Le factoriel d'un nombre est ce nombre multiplié par tous les entiers strictement positifs inferieurs à lui; c'est toujours pas clair? Bien passons aux exemples:
3! = 6 car 3! correspond à 3*2*1 de même, le factoriel de 17 sera 17*16*15*14*13*12*11*10*9*8*7*6*5*4*3*2*1 mais là de tête, bien qu'étant en Terminale S j'ai du mal ^^
voilà j'espère que ça vous aide tous.
PS: Vénitien tu as oublié de fermer une parenthèse dans ton calcul. Et si tu trouves un moyen pour Daisuke, je suis également preneur.
Daisuke => je pense que pour la meule on peut considerer ca comme une pioche, à ceci près que tu te défausses de cette carte.
Note : 10/10
68 points
Le 08/01/2010
J'ai du m'y reprendre plusieurs fois pour le comprendre, mais cette fois, je crois que c'est bon.
Sinon du haut de mes 14 ans, je pense avoir compris.
Super article !!!
Note : 10/10
1187 points
Le 08/01/2010
Oui certes mais tous nos sectataires sont pas en terminal S.. T'en fais quoi des plus jeunes et des vieux grabataires comme moi qu'ont plus de mémoires
66666 points
Le 06/01/2010
Elvorfilio : Ben il suffit de multiplier par 100
Je suis en prépa maths sup...
et il me semble que les probas, on les voit déjà en terminale S
1187 points
Le 06/01/2010
Bien que les proba m'ont toujours fasciné, j'y ai jamais rien compris.
Juste pour savoir, les valeurs de proba à gauche pourrait pas être affichée en % Svp, histoire de faciliter la lecture du graphe.?
254 points
Le 05/01/2010
Daisuke -> J'aurais bien rentré ces paramétres, mais ça devient bien vite un truc trés trés trés lourd :s Et si j'ai biens compris d'autres com's, je me serais même trompé dans mon affichage de formule (les graphes sont bons eux, no probs). Bref, ca devient trop compliqué... Mais si tu fais des maths, tu peux te lancer dedant
Lyriel -> Comme ont dit les autres: compte les précepteurs comme étant une carte supplémentaire, tout en gardant à l'esprit que tu mettra géneralement un tour en plus. Il vaut parfois mieux mettre un piocheur (en noir par exemple, Signature de sang), et c'est comme si tu faisais un bond de X tours dans le graphe (X cartes piochées). Et oui, tu est tout excusé si tu n'as pas compris les maths Par contre, je ne rembourse pas les claviers d'ordi remplis de ... enfin, cf le paragraphe en question pour comprendre XD
66666 points
Le 05/01/2010
Lyriel --> Oui, ajouter des tuteurs dans ce genre augmente nettement tes chances d'obtenir la carte que tu veux. Tu peux quasiment considérer que le nombre de cette carte dans ton deck est égal à son nombre réel (généralement 4, mais bon, pas toujours) + le nombre de tuteurs... Avec la restriction suivante, qui est que le tuteur te fera généralement perdre un tour (vus les manas qu'il consomme, ou le fait qu'il mette la carte au-dessus de ta bibliothèque et non dans ta main, avec Lilianna).
Moi je vous ferai peut-être un article sur les probabilités de piocher telle ou telle carte en Highlander. Et je vous expliquerai pourquoi il vaut mieux ne mettre chacune qu'en un seul exemplaire.
608 points
Le 05/01/2010
Lyriel, si les cartes "précepteur démoniaque" et "Liliana Vess" ne te servent pas dans ta combo, tu peux faire comme si ces cartes-là était un exemplaire en plus de ta carte en fait. Mais à prendre avec des pincettes, car, supposons que tu veuilles tirer un nocturnus vampire, tu en mets 4 dans ton deck et tu as 4 précepteurs et 4 Liliana, c'est comme si tu avais 12 Nocturnus. Sauf que quand tu tires un précepteur, et que tu l'utilises, tu enlêves 2 cartes d'un coup: le précepteur et un des nocturnus. C'est juste que si tu tires les 4 exemplaires de ton Nocturnus ils n'y a plus d'exemplaires, donc les autres précepteurs ne servent plus à rien. Je ne sais pas si je suis assez clair...
89 points
Le 05/01/2010
euh... si on est en étude littéraire, est ce qu'on a une excuse pour n'avoir compris que la partie paragraphée ?
En tout, cas très bon article. Encore que tu n'a pas fait que du calcul pour les explication sinon je serais déjà K.O.
Cependant, j'ai une question. Je joue pas mal de Précepteur démoniaque dans mon deck ainsi que des Liliana. Cela augmente donc mes chance de trouver La carte sur laquelle repose mon deck, non ?
Note : 10/10
12 points
Le 05/01/2010
Sinon, superbe article tout simplement! Même s'il ne sert pas à grand chose durant les partie si on se rappelle que 45!=119622220865480194561963161495657715064383733760000000000... Enfin, peut être qu'il y a une possibilité de simplifier le calcul...(Malheureusement, on divise pas (60-n-t)² et non (60-n)...)
Note : 10/10
608 points
Le 05/01/2010
Venitien, j'adore ton article! J'ai toujours voulu construire un modèle statistique dynamique pour Magic, juste pour le fun (je suis en CPGE MP cette année et je compte faire des maths pour gagner ma vie, même si ça sera plus dans la théorie des nombres ), je vois que ton modèle ne prend en compte que les jeux où il n'y a pas de piocheurs, pas de moyen de faire meuler (que ce soit toi ou l'adversaire), qu'ajouterais tu pour construire un système dynamique? Je veux dire, un système avec lequel on puisse modéliser en temps réel les chances de tirer nos cartes (c'est-à-dire en considérant ce que l'on a en main, faut penser aux piocheurs...)
Note : 10/10
66666 points
Le 05/01/2010
Je suis pas d'accord avec toi Vénition, puisqu'il faudrait commencer par savoir combien de terrain il avait mis dans son deck, afin d'estimer à partir de quel tour il avait 7 terrains de disponible.
D'ailleurs, il ne parle pas de 7 terrains, mais de 7 manas dispo, donc suivant les accélérateurs de mana, les sorts de pioches qui ont été joué, etc. c'est très difficile pour ne pas dire impossible d'estimer la probabilité que la partie se finisse dans cette situationà partir des informations qu'il donne.
Cependant, ce n'est pas la question, la question est de savoir, étant donnée la situation, la proba pour que la prochaine carte top-deckée soit la carte en question. C'est tout simplement le rapport du nombre d'exemplaires de la carte dans le deck sur le nombre de cartes restantes dans le deck à ce moment là, donc 2/X. Toute la question est donc d'estimé ce X, ce que j'aurais bien fait en utilisant la formule fournie, mais j'ai l'impression qu'elle est mal recopiée (il manque au moins un crochet en tout cas)
Bien entendu, la loi de Murphy appliquée à Magic implique que cette probabilité est en fait de 100%, à condition qu'il n'existe aucun moyen de faire durer la partie un tour de plus.
J'avais un article de ce genre dans mes cartons (je parlais aussi des proba d'avoir une certaine carte en ouvrant un booster, ou des autres aspects aléatoires de Magic, notamment le pile-ou-face, qui est plus simple à traiter), mais bon, comme ça, c'est fait ^^
254 points
Le 05/01/2010
Alors effectivement, il suffit pas de mettre les cartes comme ça dans les slives, de mélanger le tout et de piocher pour dire qu'on va gagner avec X proba... Il faut également construire son deck avec intelligence, et le jouer de façon malgne, mais y'a déja un paquet d'articles là-dessus Il s'agit plus d'une petite curiosité.
Rincevent -> Donc, tu dis que au 7é tour, tu est mort, donc t'avais pioché 14 cartes, ça veut dire qu'il en restait 106 dans ta bibli. Alors, normalement, c'est P(A/B), ou la proba que la carte était la 107é sachant que t'avais eu la 1é... Pour pas faire compliqué, on va dire que les chances de piocher chaque cartes sont indépendantes. Ca te faisait donc une chance sur 120, puisqu'il y a une chance sur 120 que la carte manquante soit en 107é position dans ta bibli. Enfin, je crois...
6574 points
Le 05/01/2010
C'est une bonne chose d'avoir une certaine idée de ces proba quand on construit un deck, surtout si on joue beaucoup sur les combos. À mon avis il vaut mieux bien regarder les chances qu'on a de ne pas réunir les cartes plutôt que d'estimer que 60 % en principe c'est bon et de pleurnicher ensuite que le jeu ne sort pas.
Toutefois il ne faut pas uniquement se référer à cela pour choisir s'il on met telle ou telle carte et en combien d'exemplaires, il faut se demander si la carte en question est utile seule, si plusieurs exemplaires ensembles ont un intérêt, si elle est facile à envoyer au cimetière, si on l'a en plusieurs illustrations différentes (essentiel), etc...
Petit problème :
La semaine dernière, j'ai joué avec un deck d'environ 120 cartes contenant 2 cartes en 1 exemplaire chacune qui constituent ensemble une combo imparable pour gagner, à condition d'avoir au moins 7 manas.
Sachant que je suis mort avec plus de 7 manas disponibles et l'une des deux cartes en main, quelle était la probabilité pour que la carte suivante de ma bibliothèque soit l'autre carte de la combo, comme cela s'est produit ?